baekjoon 12781:PIZZA ALVOLOC

baekjoon 12781 PIZZA ALVOLOC

12781번 PIZZA ALVOLOC

접근

ccw 알고리즘을 사용한다. ccw(counter clock wise)는 2차원에 있는 세점에 대해 서로의 상대적 위치를 나타낸다.

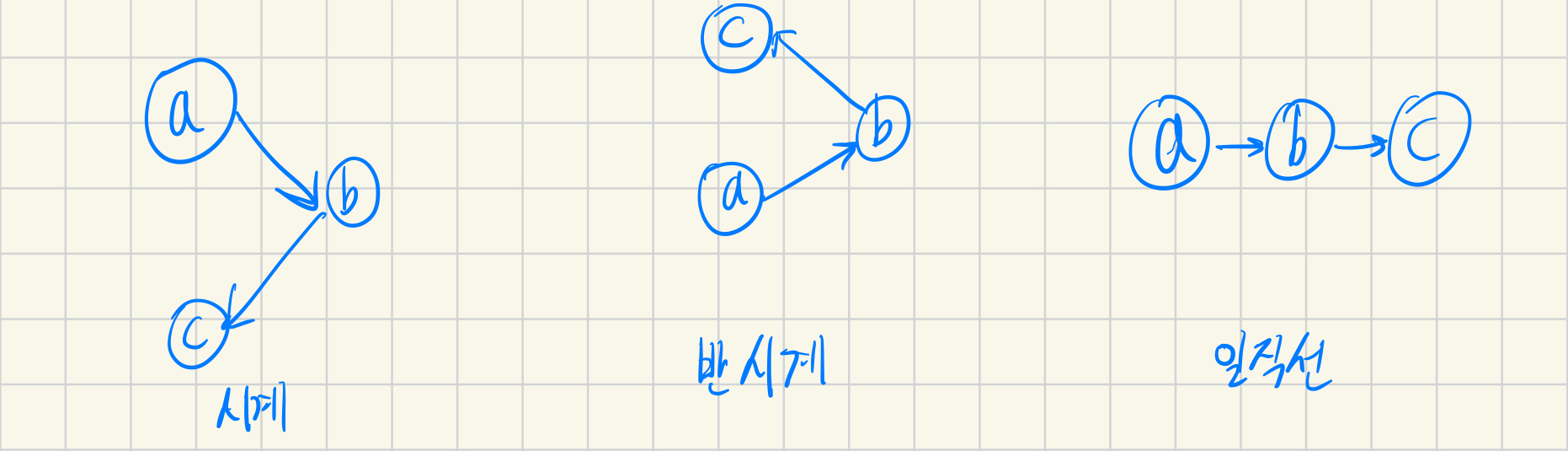
그리고 ccw는 외적을 이용해서 이를 구해낸다.
오른 나사 법칙에 의해 xyz공간에 xy평면에 세 점이 있다고 치면 두 벡터의 외적 결과의 z방향의 부호가 달라진다.
(원래는 2차원은 외적 안된다. z성분 0 가정 후 외적하는 거임)

1. 시계 < 0
2. 반시계 > 0
3. 일직선 == 0

\[\begin{bmatrix} x_{2}-x_{1} \\y_{2}-y_{1} \\0 \end{bmatrix}\times \begin{bmatrix} x_{3}-x_{2}\\ y_{3}-y_{2} \\0 \end{bmatrix}=(x_{1}y_{2}+x_{2}y_{3}+x_{3}y_{1})-(x_{1}y_{3}+x_{2}y_{1}+x_{3}y_{2})\]

ccw결과의 부호만 필요하다.

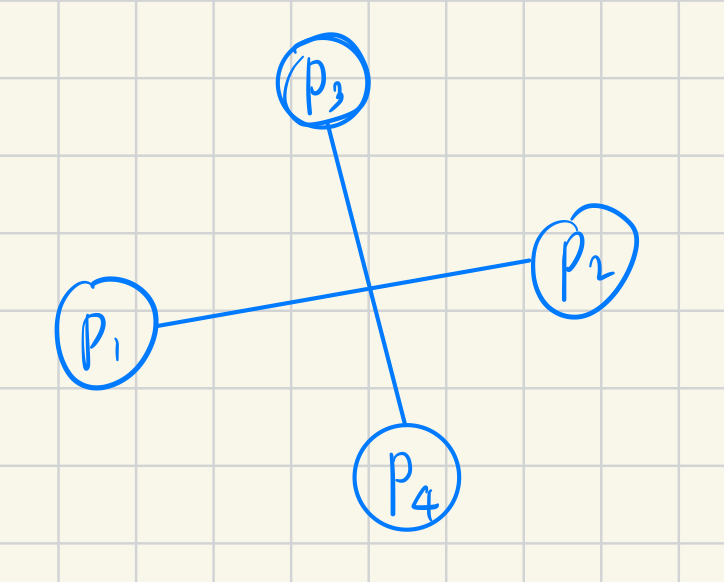
2점을 이은 선분이 교차 하는 것은 이런 모습이다.
여기서 교차하여 점을 만든다는 것은 한 선분에 대해 나머지 두 점이 반대 방향에 있어야 한다.
따라서

\(ccw(p_{1}, p_{2}, p_{3})\times ccw(p_{1}, p_{2}, p_{4}) \le 0 \text{ && }ccw(p_{3}, p_{4}, p_{1})\times ccw(p_{3}, p_{4}, p_{2})\le 0\) 이 성립한다.
여기서 == 0은 세점이 일직선에 있는 경우 혹은 네 점이 일직선에 있는 경우 혹은 두 점이 겹치는 경우인데
모두 문제에서 해당되지 않으니 이 문제에선 제거해줘야 한다. 원래는 ccw가 모두 0인 경우는 예외처리를 해야한다.

코드

#include <iostream>
#include <array>
using namespace std;
int ccw(pair<int, int> a, pair<int, int> b, pair<int, int> c){
  int temp = a.first*b.second + b.first*c.second + c.first*a.second - a.second*b.first - b.second*c.first - c.second*a.first;
  if(temp > 0) return 1;
  else if(temp < 0) return -1;
  else return 0;
}
int main(){
  ios::sync_with_stdio(false);
  cin.tie(0); cout.tie(0);
  array<pair<int, int>, 4> p;
  cin >> p[0].first >> p[0].second >> p[1].first >> p[1].second >> p[2].first >> p[2].second >> p[3].first >> p[3].second;
  //끝점 포함 x여야함.
  
  int v1 = ccw(p[0], p[1], p[2]);
  int v2 = ccw(p[0], p[1], p[3]);
  int v3 = ccw(p[2], p[3], p[0]);
  int v4 = ccw(p[2], p[3], p[1]);
  if(v1*v2 < 0 && v3*v4 < 0){ //0이된다는건 한 끝점이 다른 끝점에 들어간다는 건데 그럼 안됨.
    cout << 1;
  }
  else cout << 0;
  return 0;
}

배운 점

ccw를 배웠다.