baekjoon 1931:회의실 배정

baekjoon 1931 회의실 배정

1931번 회의실 배정

접근

회의실 배정은 유명한 그리디 알고리즘 문제이다.

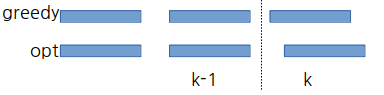
k-1번째까지만 greedy랑 optimal solution이랑 같다고 해보자.
greedy는 항상 일찍 끝나는 것을 고르니 optimal solution의 k번째 회의보다 더 먼저 끝나는 k번째 회의를 가지고 있을 것이다.
그런데 optimal solution의 k번째를 greedy의 k번째로 바꿔도 더 먼저 끝나기 때문에 뒤에 따라오는 k+1, k+2번째에 영향을 주지 않고
총 회의 개수는 무조건 동일하게 유지된다. 그럼 greedy도 opt sol이 될 수 있는 것이고
따라서 greedy랑 optimal solution이랑 k번째까지만 같다는 것은 모순이다.

코드

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;
bool compare1(pair<int, int> a, pair<int, int> b) { //vector의 비교 함수를 따로 제작하였다.
  if (a.second < b.second) {
    return true;
  }
  else if (a.second == b.second) {
    return a.first < b.first;
  }
  else{
    return false;
  }
}
int main(){
  ios::sync_with_stdio(false);
  cin.tie(0); cout.tie(0);

  int n; cin >> n;
  vector<pair<int, int>> v;
  while(n--){
    int a, b;
    cin >> a >> b;
    v.push_back({a, b});
  }
  sort(v.begin(), v.end(), compare1); //먼저 끝나는 회의를 고르기 위해 끝나는 시간 기준 오름차순으로 미리 회의를 정렬한다.
  int count = 0;
  int endtime = 0;
  for(int i = 0; i < v.size(); i++){
    if(endtime <= v[i].first){
      count++;
      endtime = v[i].second;
    }
  }
  cout << count;
  
  return 0;
}

배운 점

greedy알고리즘 실제 구현해보고, vector 정렬 함수 따로 제작 해서 하는 방법을 배웠다.