baekjoon 1967:트리의 지름

baekjoon 1967 트리의 지름

1967번 트리의 지름

접근

처음엔 dp로 풀까도 생각 했는데 너무 경우의 수가 많아진다. 그래서 결국 찾아보니 dfs두번 돌아서 푸는 문제라고 한다.
임의의 루트노드에서 가장 먼 점을 찾는다. 그 점이 트리의 지름의 한점에 들어간다.
그 점에서 다시 dfs를 돌려서 그 점에서 가장 먼 점을 찾는다. 두 점이 트리의 지름을 이룬다.
밑줄 친 문장이 보장된다면 그 점에서 dfs돌려서 가장 먼 점을 지름의 다른 끝 점으로 잡는건 자연스러운 생각이다.
그렇다면 왜? 임의의 루트노드에서 가장 먼 점을 찾았을 때 그 점이 트리의 지름에 들어가는지를 증명해야한다.

1. 한점이 같을 때
2. 중간 경로가 겹칠 때
3. 경로가 하나도 안 겹칠 때
   
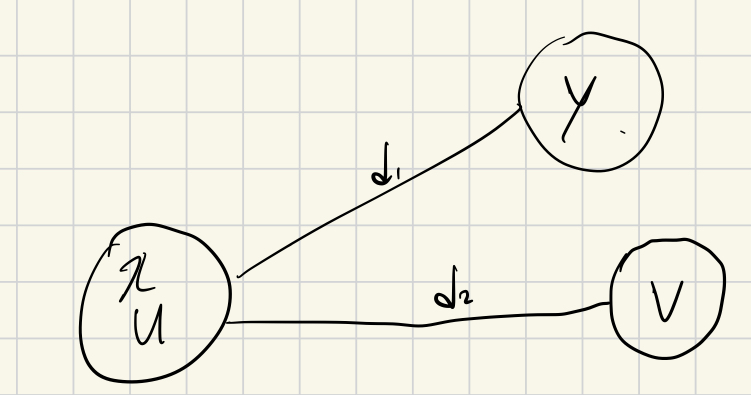
   1번 경우: 임의의 정점 x에서 찾은 최장거리 정점 y이다. (u, v)은 지름이다. x=u, y!=v이라
   한다면 y가 x의 최장거리니까 d1>=d2 ==> 모순이다.
   
   
   
   
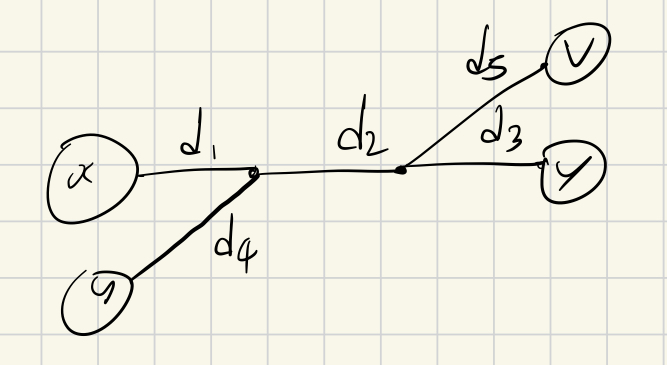
   2번 경우: y가 가장 멀어야하니 d5 <= d3.
   그럼 u입장에서 v가 아니라 y를 지름점으로 잡았겠지 ==> 모순이다.
   
   
   
   
   
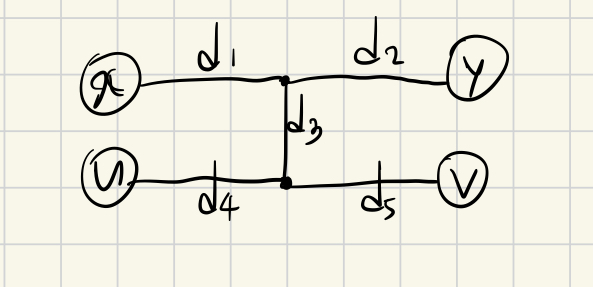
   3번 경우: y가 가장 멀어야하니 d2 >= d3 + max(d4, d5)
   그럼 u입장에서 d2+d3>=d5 이므로 v말고 y를 지름점으로 잡았겠지 ==> 모순이다.
   
   
   

   코드

#include <iostream>
#include <vector>
using namespace std;
void dfs(vector<vector<pair<int, int>>>& v, int x, vector<int>& dist);
int main(){
  ios::sync_with_stdio(false);
  cin.tie(0); cout.tie(0);
  int n; cin >> n;
  vector<vector<pair<int, int>>> v(n); //가중치 그래프 만드는 법
  vector<int> dist(n, -1); 
  for(int i = 0; i < n-1; i++){
  int a, b, c; cin >> a >> b >> c;
    v[a-1].push_back({b-1, c});
    v[b-1].push_back({a-1, c}); //무방향-->양방향
  }
  dist[0] = 0;
  dfs(v, 0, dist);
  int u = 0;
  int max = 0;
  for(int i = 0; i < n; i++){
    if(dist[i] > max){
      max = dist[i];
      u = i;
    }
  } //dfs돌아서 가장 먼 점 찾기(1)
  fill(dist.begin(), dist.end(), -1);
  dist[u] = 0;
  dfs(v, u, dist);
  int max2 = 0;
  for(int i = 0; i < n; i++){
    if(dist[i] > max2){
      max2 = dist[i];
    }
  }
  //가장 먼 점에서 또 dfs돌아서 가장 먼 점 찾기(2)
  cout << max2;
  
  
  
  
  return 0;
}
void dfs(vector<vector<pair<int, int>>>& v, int x, vector<int>& dist){
  for(auto& i : v[x]){
    if(dist[i.first] == -1){
      dist[i.first] = dist[x] + i.second;    
      dfs(v, i.first, dist);
    }
  }
}

추가로 생각할 점

tree는 모든 두 점 사이의 경로가 한가지로 결정된다. 그래서 트리 안에서 dfs를 돌리든, bfs를 돌리든, dijkstra를 돌리든 모든 점을 한번씩만 방문하게 되고
그 때 결정한 거리가 최단거리가 된다.(경로가 하나니까)